Around the Hull-White short-rate model
Introduction
Disclaimer : this is the summary of a project done with 2 friends for Pr Jiao Ying in 2017. The corresponding code is avaliable here. Sorry but the following is in french.
Nous allons traiter ici le modèle d’Hull et White, développé à partir du modèle de Vasicek en 1990. Nous commencerons par quelques prérequis, notamment le modèle de vasicek ainsi que des considérations sur les processus d’Ornstein-Uhlenbeck correspondant, avant de nous attaquer au modèle HW en lui-même. Rappelons que nous nous plaçons dans un modèle de marché parfait (infinie liquidité des actifs, coûts de transaction nuls, actifs infiniment divisibles notamment).
Le modèle de vasicek et quelques pré-requis
Rappelons ici la dynamique du taux court dans le modèle de vasicek:
Sous le modèle de vasicek, le taux court suit la dynamique suivante:
\(dr_{t} = a(b-r_{t})dt + \sigma dW_{t}\)
Avec :
\(a\) constante positive, représentant la force de rappel
\(b\) constante positive, représentant le taux long terme
\(\sigma\) constante positive, représentant la volatilité
On pourrait tout a fait noter \(\vartheta= ab\), les paramètres du modèle devenant alors \(\vartheta\), \(a\) et \(\sigma\)
Sous vasicek, le taux court suit un processus d’Ornstein-Uhlenbeck, et la solution correspondante est :
\(r_t = r_0 e^{-at} + b(1-e^{-at}) + \sigma e^{-at} \int_0^t e^{au} dW_u\) \[O-U\]
A t fixé, ce processus d’Ornstein-Uhlenbeck suit une loi gaussienne de paramètres son espérance et sa variances, un processus d’Ornstein-Uhlenbeck est en effet à la fois Gaussien et Markovien.
Soit \(X\) une variable aléatoire suivant une loi normale. Alors \(e^X\) suit une loi log-normale et donc :
\(\mathbb{E}(e^X) = e^{\mathbb{E}(X) + \frac{1}{2} \mathbb{V}(X)}\)
Le modèle de Hull et White
Développé par J.C.Hull et A.White a partir de 1990, le modèle Hull-White est encore très utilisé sur le marché aujourd’hui. L’objectif premier de ce modèle était de correspondre exactement aux données de marché afin de d’obtenir une courbe des taux dans le modèle correspondant exactement à la courbe empirique des taux "réels" fournie par le marché. L’intuition fut la suivante : ajouter un paramètre (non-stochastique) dépendant du temps dans le drift de la dynamique du taux d’intérêt. La mise en oeuvre de ce modèle nécessite une paramétrisation (le paramètre non-stochastique ajouté) à partir des données de marché.
Dans l’extension proposée par Hull-white du modèle de vasicek, c’est le paramètre \(\vartheta\) qui devient une fonction déterministe du temps :
Sous le modèle Hull-White, le taux court suit la dynamique suivante :
\(dr_{t} = (\vartheta_{t}-ar_{t})dt + \sigma dW_{t}\)
Avec :
\(a\) constante positive, représentant la force de rappel
\(\vartheta_{t}\) une fonction déterministe du temps
\(\sigma\) constante positive, représentant la volatilité
Par intégration (via le lemme d’Ito) de la dynamique du taux court sous Hull-White, on obtient: \[r_t = r_{s}e^{-a(t-s)}+\int_s^t e^{-a(t-u)}\vartheta_u du + \sigma \int_s^t e^{-a(t-u)}dW_u\]
On a: \[\begin{aligned} d(r_{t}e^{at}) &= r_{t}e^{at}adt + e^{at}dr_{t} \\ &= r_{t}e^{at}adt + e^{at}\vartheta_{t}dt - r_{t}e^{at}adt + e^{at}\sigma dW_{t} \\ &= e^{at}(\vartheta_{t}dt+\sigma dW_{t}) \end{aligned}\]
Ce qui implique que :
\(r_{t}e^{at} = r_{s}e^{as}+\int_s^t e^{au}\vartheta_u du + \sigma \int_s^t e^{au}dW_u\)
et donc :
\(r_t = r_{s}e^{-a(t-s)}+\int_s^t e^{-a(t-u)}\vartheta_u du + \sigma \int_s^t e^{-a(t-u)}dW_u\)
Sous le modèle Hull-White, le prix d’un zéro-coupon est donné par : \[B(t,T)=exp(\frac{ r_t (1-e^{-a(T-t)})}{a} - \frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du + \frac{1}{2}[\int_t^T \frac{{\sigma}^2}{a^2}(1-e^{-a(t-u)^2} du)])\]
On commence par calculer \(\int_t^T r_s ds\) directement à partir de la dynamique de r : \[\begin{aligned} r_T - r_t & = \int_t^T \vartheta_u - a r_u du + \int_t^T\sigma d W_u \\ & = \int_t^T \vartheta_u du - \int_t^T ar_u du + \sigma\int_t^T dW_u \end{aligned}\] Remarquons que grâce a la propriété précédente,
\[\begin{aligned} r_T - r_t & = r_{t}e^{-a(T-t)}+\int_t^T e^{-a(T-u)}\vartheta_u du + \sigma \int_t^T e^{-a(T-u)}dW_u - r_t \\ & = -r_{t}(1-e^{-a(T-t)})+\int_t^T e^{-a(T-u)}\vartheta_u du + \sigma \int_t^T e^{-a(T-u)}dW_u \\ \end{aligned}\]
Que l’on injectera dans notre équation : \[\begin{aligned} a \int_t^T r_u du & = \int_t^T \vartheta_u du - ( r_T - r_t ) + \sigma\int_t^T dW_u \\ & = \int_t^T \vartheta_u du - ( - r_{t}(1-e^{-a(T-t)})+\int_t^T e^{-a(T-u)}\vartheta_u du + \sigma \int_t^T e^{-a(T-u)}dW_u )+ \sigma\int_t^T dW_u \\ & = r_{t}(1-e^{-a(T-t)}) + \int_t^T \vartheta_u (1-e^{-a(T-u)}) du + \sigma \int_t^T (1-e^{-a(T-u)}) dW_u \end{aligned}\] Finalement, on a: \[\int_t^T r_u du = \frac{ r_t (1-e^{-a(T-t)})}{a} + \frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du + \frac{\sigma}{a} \int_t^T (1-e^{-a(T-u)}) dW_u\] Calculons son espérance, en notant que l’intégrale sur le brownien est une martingale (d’espérance nulle) : \[\begin{aligned} \mathbb{E}[\int_t^T r_u du | \mathcal{F}_t] & = \frac{ r_t (1-e^{-a(T-t)})}{a} + \frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du + \underbrace{\mathbb{E}[\frac{\sigma}{a} \int_t^T (1-e^{-a(T-u)}) dW_u|\mathcal{F}_t]}_{=0}\\ & = \frac{ r_t (1-e^{-a(T-t)})}{a} + \frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du \end{aligned}\] Ainsi que sa variance :
\(Var[\int_t^T r_u du | \mathcal{F}_t] = Var[ \underbrace{\frac{ r_t (1-e^{-a(T-t)})}{a}}_{deterministe} + \underbrace{\frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du}_{deterministe} + \underbrace{\frac{\sigma}{a} \int_t^T (1-e^{-a(T-u)}) dW_u}_{stochastique}]\)
Et ainsi : \[\begin{aligned} Var[\int_t^T r_u du | \mathcal{F}_t] & = Var[\frac{\sigma}{a} \int_t^T (1-e^{-a(T-u)}) dW_u] \\ & = \int_t^T \frac{{\sigma}^2}{a^2}(1-e^{-a(t-u)})^2 du \end{aligned}\]
Comme \(\int_t^T r_u du | \mathcal{F}_t\) est un processus d’Ornstein-Uhlenbeck, on utilise la propriété O-U, et on obtient : \[\begin{aligned} B(t,T) & = \mathbb{E}[e^{-\int_t^T r_s ds}|\mathcal{F}_s] \\ & = exp(-\mathbb{E}[\int_t^T r_u du | \mathcal{F}_t] + \frac{1}{2}Var[\int_t^T r_u du | \mathcal{F}_t]) \\ & = exp(\frac{ r_t (1-e^{-a(T-t)})}{a} - \frac{1}{a}\int_t^T \vartheta_u (1-e^{-a(T-u)}) du + \frac{1}{2}[\int_t^T \frac{{\sigma}^2}{a^2}(1-e^{-a(t-u)^2} du)]) \end{aligned}\]
Ainsi, nous avons pu complètement définir le prix de n’importe quel zéro-coupon. Pour des raisons de simplification des calculs, nous prendrons les notation suivante :
\(\forall t,T, A(t,T) = \frac{1-e^{-a(T-t)}}{a}\)
\(\forall t,T, C(t,T) = - \int_t^T \vartheta_u A(u,T) + \frac{ \sigma^2 A(u,T)^2}{2} du\)
Et le prix du zéro coupon s’écrit alors :
\(B(t,T) = \exp{ - r_t A(t,T) + C(t,T)}\)
On voit ici que le modèle de Hull-White à un facteur est bien un modèle affine, étant donné que \(\exp{C(t,T)}\) et \(A(t,T)\) sont des fonctions déterministes.
Pour en arriver a notre but (construire la courbe des taux), nous allons maintenant déduire du prix du zéro-coupon le prix des taux moyens continus :
\[Taux d'intérêt continu moyen\] Par définition, le taux d’intérêt continu moyen s’écrit : \[R(t,T) = \frac{-1}{T-t} ln(B(t,T))\]
Ici, on a : \[R(t,T) = \frac{-1}{T-t} ( - r_t A(t,T) + C(t,T))\]
Simulations
Pour l’ensemble des simulations suivantes, nous avons arbitrairement
fixé :
\(a=0.5\), \(\sigma=1\), \(r_0 = 0\) et \(\vartheta(t) = 1-\frac{\sin(10t)}{t+1}\)
Comme présenté précédemment, la mise en oeuvre de ce modèle nécessité une paramétrisation de \(\vartheta\) à partir des données de marchés. Nous choisirons des fonctions simples pour \(\vartheta\), sans pousser plus loin la paramétrisation du modèle avec les données de marché.
On fixe le nombre de discrétisation de notre brownien \(n\).
Soit \(W\) notre vecteur contenant les valeurs du mouvement brownien
\(W_{0}=0\) et pour \(i\) de \(1\) à \(n-1\) :
\(W_{i+1} = W_{i} + \frac{1}{n} \cdot \eta\)
Avec \(\eta\) une réalisation d’une \(\mathcal{N}(0,1)\) pour chaque
itération de \(i\).
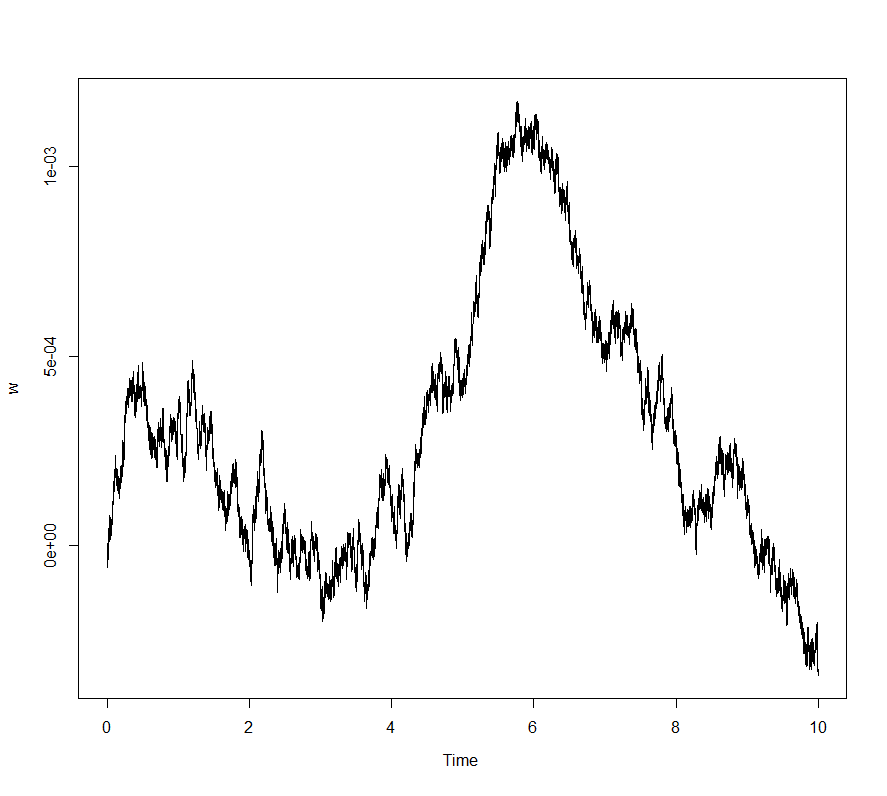
Simulation d’un mouvement brownien sur 10 ans avec 1 000 000 itérations
Simulation du taux court
Maintenant que nous avons un brownien standard, nous pouvons nous en servir pour simuler le taux court \(r_{t}\).
On fixe \(a\), \(\sigma\) et \(\vartheta\).
On génère un mouvement brownien \(W\).
\(tmp_1\) reçoit le calcul numérique de
\(\int^{t}_{0}e^{-a\cdot(t-u)}\cdot \vartheta(u) du\).
On décompose :
\(\int^{t}_{0}e^{au}dW_{u} = e^{at}W_{t} - \int^{t}_{0}a \cdot e^{au} \cdot W_u du\).
\(tmp_2\) reçoit le calcul numérique de
\(\int^{t}_{0}a \cdot e^{au} \cdot W_{u} du\) (méthode des rectangles par
exemple).
\(r_{t}\) reçoit finalement
\(r_{0} \cdot e^{-at} + tmp_{1} + \sigma e^{-at} \cdot (e^{at} \cdot W_{t} - tmp_{2})\).
Le graphique suivant représente le taux court en fonction du temps \(t\) ainsi que de nos paramètres fixés préalablement. Notons que notre fonction \(\vartheta\) nous permet d’obtenir un taux court qui croît globalement et qui oscille légèrement pour enfin visiblement converger (car \(\vartheta\) est bornée).
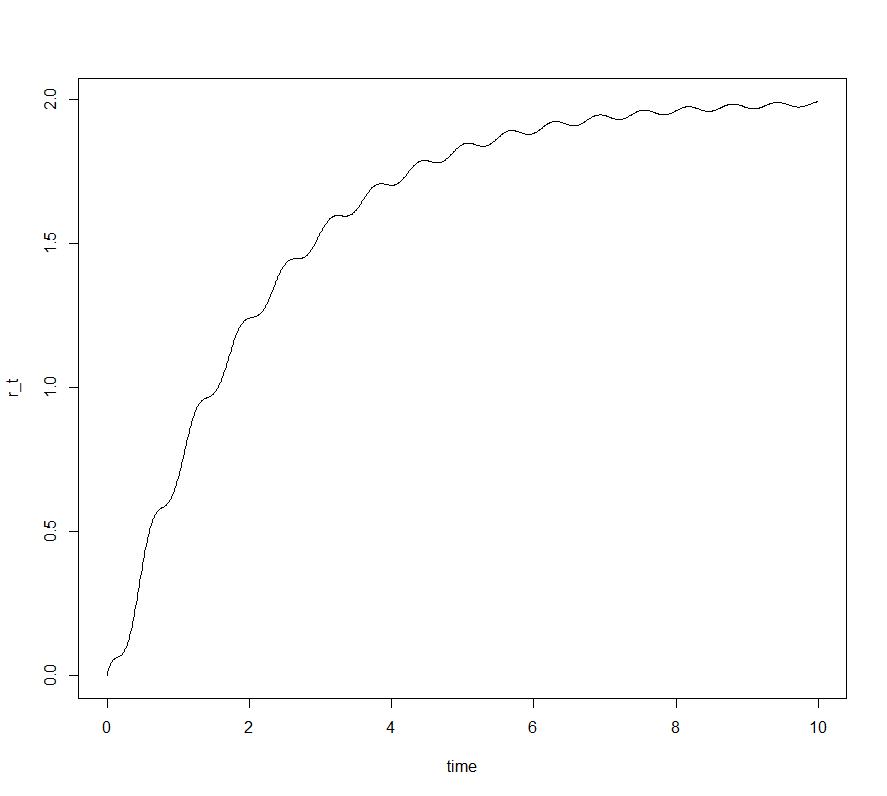
Simulation d’un taux court sur 10 ans avec 1 000 000 de discrétisations du brownien sousjacent
L’intérêt de la fonction sinus dans \(\vartheta\) était d’avoir un caractère oscillatoire dans notre taux court, l’idée étant de se rapprocher de la réalité sans aller plus loin dans la paramétrisation.
Simulation du prix du zéro-coupon \(B(0,T)\)
Si \(T=0\) alors \(B(0,T)=1\).
On déclare \(A(t,T,a) = \frac{1}{a} \cdot (1 - e^{-a\cdot (T-t)})\) Comme
\(r_{0} = 0\), cela nous épargne le calcul de
\(tmp_{1} = r_{0} \cdot A(0,T,a)\).
\(tmp_{2}\) reçoit le calcul numérique de
\(\int^{T}_{0} \vartheta(s) \cdot A(s,T,a) ds\)
\(tmp_{3}\) reçoit le calcul numérique de
\(\frac{1}{2} \cdot \sigma^{2} \cdot \int^{T}_{0}A(s,T,a)^2ds\)
Enfin on a \(B(0,T)=e^{tmp_{1} - tmp_{2} + tmp_{3}}\)
Le graphique suivant représente donc le prix d’un zéro-coupon \(B(0,t)\) en \(0\) en fonction de sa maturité \(T\). Notons qu’ici le taux court n’est pas exploité.
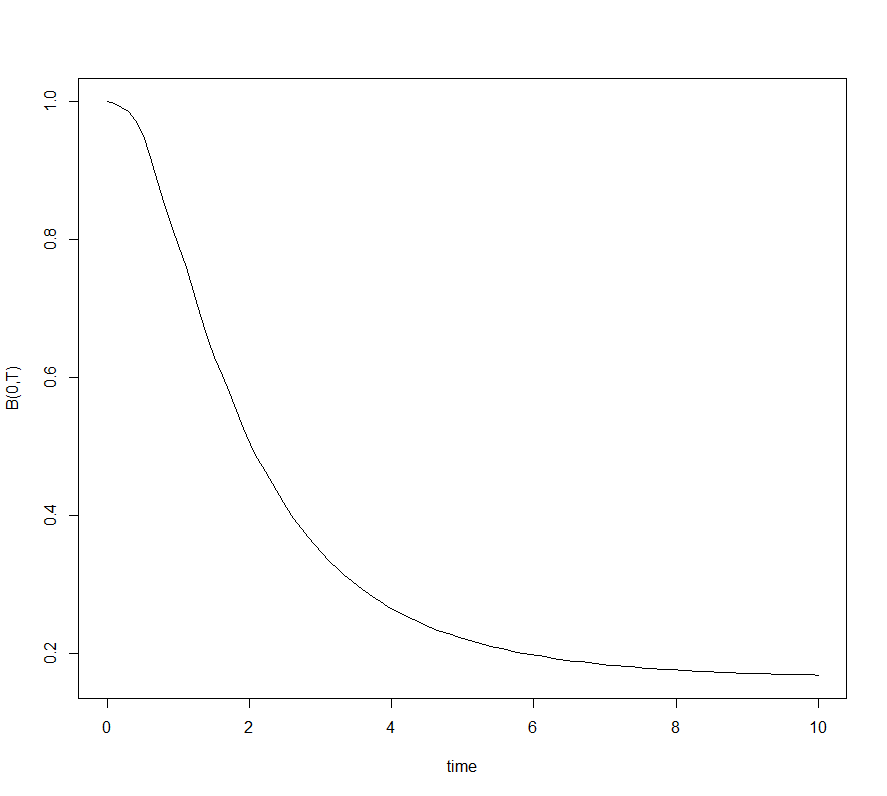
Simulation du prix d’un zéro-coupon de maturité \(T\)
Il est cohérent d’obtenir une fonction décroissante en T en t=0 fixé pour des taux d’intérêt positifs.
Et le suivant représente le prix d’un zéro-coupon \(B(t,T)\)
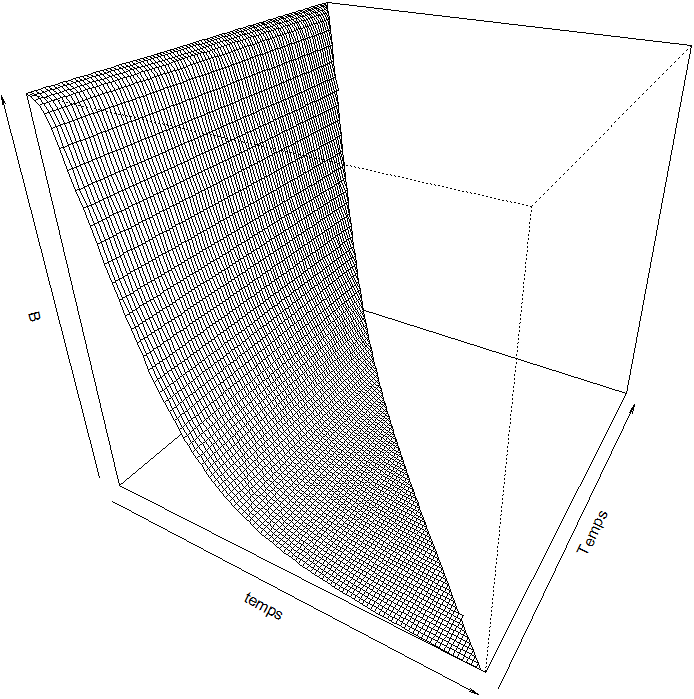
Simulation de la courbe des taux B(temps,Temps) sur 10 ans
Simulation et graphe de la courbe de taux
Maintenant que nous sommes capables de calculer le prix du zéro-coupon, il ne reste plus qu’à l’inclure dans le calcul des valeurs de la courbe des taux pour enfin pouvoir en sortir une surface.
\(R(0,T) = -\frac{1}{T} \cdot \log(B(0,T))\)
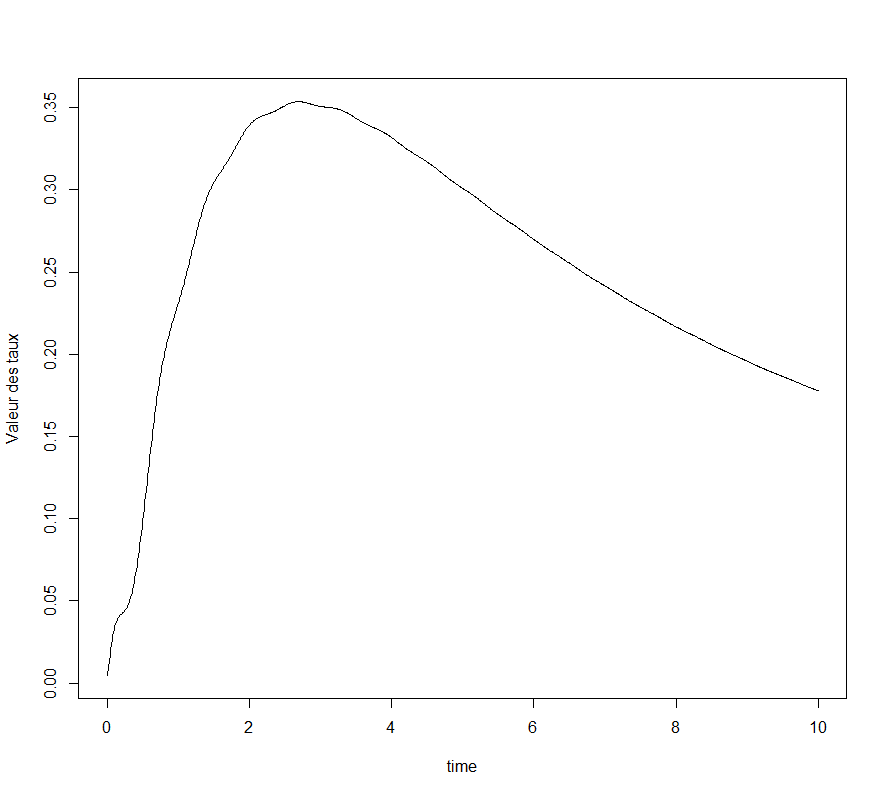
Simulation de la surface des taux en \(t=0\) sur 10 ans
Nous obtenons bien une courbe des taux concave. Néanmoins, il se trouve
que notre courbe de taux finit par être décroissante à partir de \(3\)
ans. Cette caractérisation contre intuitive est très probablement due à
la paramétrisation de notre modèle.
Enfin, le graphique suivant représente la surface des taux.
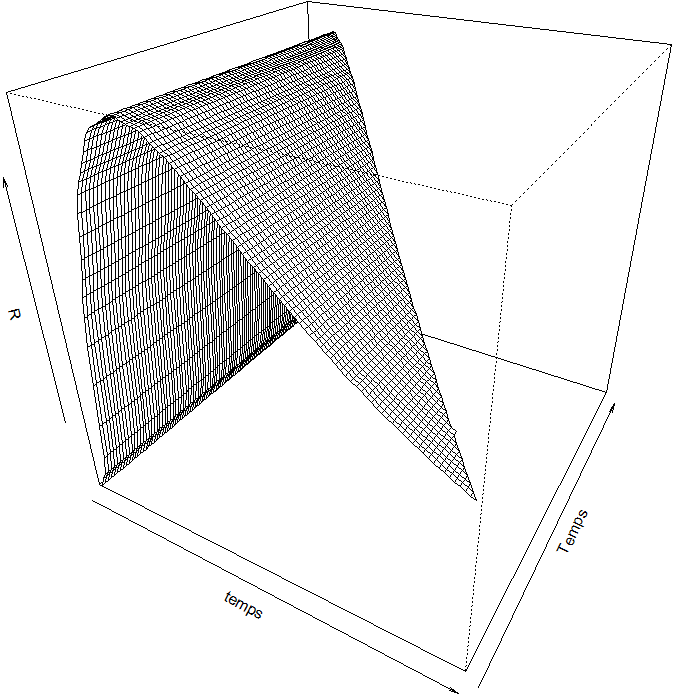
Simulation de la surface des taux R(temps,Temps) sur 10 ans
Conclusion
Naturellement, nous n’avons pas pu aller plus loin dans l’analyse financière de nos résultats car nous sommes limités par la sélection des paramètres. Pour calibrer un tel modèle, on pourra citer "Calibration Methods of Hull-White Model" article de Sebastien Gurrieri, Masaki Nakabayashi et Tony Wong parut en 2011.
Annexes
Ci-dessous le code que nous avons utiliser pour générer les graphiques. Nous avons utiliser une méthode de Monte-Carlo pour calculer les intégrales stochastiques du taux court, et les formules fermées démontrées ci-dessus pour calculer les zéro-coupons et la courbe des taux.
## Simulation du brownien standard
T <- 1
n <- 100000
d <- T/n
w <- numeric(n)
for(i in 1:n) w[i+1] <- w[i] + d * rnorm(1)
## Graphique corespondant :
plot.ts(w)
abline(h = 0)
#Donc W est un brownien sur [0;n]
# parametres du modele :
.alpha = 0.5
.sigma = 1
.r0 = 0
vega <- function(t)
{
return(1- sin(10*t)/(t+1))
}
#Fonction calculans le taux court r_t :
r_t <- function(t,r0 = .r0,alpha = .alpha ,volatilite =1,periode_final=10,wienner=w)
{
# condition d'arret
if(t==0){
return(r0)
}
# Integration prerequise
max_iter <- length(w)
somme_seq <- seq(0, round(max_iter*t/periode_final,0))
N <- length(somme_seq)
somme = 0
for(i in 1:N)
{
somme = somme + exp(alpha * i * t / N) * w[i]
}
somme <- somme / N
integrale_pour_wienner <- exp(alpha*t) * w[round(max_iter*t/periode_final,0)] - alpha * somme
# return the result :
membre_2 <- integrate(function(u) return(exp(-alpha*(t-u))*vega(u)), lower = 0, upper = t)$value
membre_3 <- volatilite * exp(-alpha*t) * integrale_pour_wienner
return(r0*exp(-alpha*(t))+membre_2+membre_3)
}
#On implemente notre H&W
temps <- seq(0,10, length = 1000)
r_seq <- temps
for(i in 1:(length(temps)))
{
r_seq[i] <- r_t(temps[i])
print(c(1,i))
}
plot(temps[1:length(temps)], r_seq, type = "l", ylab = "r_t", xlab = "time")
#Fabriquons une courbe de taux
#On commence par creer la fonction qui nous donne les B(0,theta)
#B(0,theta) indexe par alpha
B <- function(t, T, alpha=.alpha, volatilite=.sigma)
{
#condition d'arret
if(T==0){return(1)}
#prerequis
A <- function(t,T,alpha=0.5){
return((1-exp(-alpha*(T-t)))/alpha)
}
#lets go
membre_1 <- r_t(t,0, alpha, volatilite)*A(t,T,alpha)
membre_2 <- integrate(function(s) return(vega(s)*A(s,T,alpha)), lower = 0, upper = T)$value
membre_3 <- 1/2 * volatilite^2 * integrate(function(s) return(A(s,T,alpha)^2), lower = 0, upper = T)$value
return(exp(- membre_1 - membre_2 + membre_3))
}
# Maintenant faisont une courbe des taux zero coupon en t=0 d'echeance entre 0 et 10 :
temps <- seq(0,10, length = 100) #t pouvant aller jusqu'a 10 ans ici
B_seq <- temps
for(i in 1:(length(temps)))
{
B_seq[i] <- B(0,temps[i])
print(c(2,i))
}
plot(temps[1:length(temps)], B_seq, type = "l", xlab = "time", ylab = "B(0,T)")
# Passons a la courbe des taux :
R <- function(t,T, alpha=.alpha,volatilite=.sigma)
{
return((-1/T) * log(B(t,T,alpha,volatilite)))
}
# Et la courbe des taux en 0 est :
temps <- seq(0,10, length = 100)
R_seq <- temps
for(i in 1:(length(temps)))
{
R_seq[i] <- R(0,temps[i])
print(c(3,i))
}
plot(temps[1:length(temps)], R_seq, type = "l", xlab = "time", ylab = "Valeur des taux")
## Maintenant, occupons nous de charter les ZC et la courbe des taux sur les deux parametres temps :
temps <- seq(0,10, length = 100)
Temps <- seq(0,10,length=100)
mat <- matrix(NA,nrow=length(temps),ncol=length(Temps))
for (i in 1:length(temps)){
for (j in 1:length(Temps)){
if((temps[i]+Temps[j]) < 10){
mat[i,j] <- B(temps[i],Temps[i])
print(c(i,j))
}
}
}
persp(temps,Temps,mat,theta=30,phi=30)
## Ensuite, la surface des taux moyens continus :
temps <- seq(0,10, length = 100)
Temps <- seq(0,10,length=100)
mat2 <- matrix(NA,nrow=length(temps),ncol=length(Temps))
for (i in 1:length(temps)){
for (j in 1:length(Temps)){
if((temps[i]+Temps[j]) < 10){
mat2[i,j] <- R(temps[i],Temps[i])
print(c(i,j))
}
}
}
persp(temps,Temps,mat,theta=30,phi=30)References :
Azizieh, Celine. 2014. “Modélisation Des Taux d’intérêt.” Université Libre De Bruxelle.
Brigo, Damiano, and Fabio Mercurio. 2006. Interest Rate Models - Theory and Practice: With Smile, Inflation and Credit. 2nd ed. Springer Finance. Springer.
Filipovic, Damir. 2009. Term-Structure Models: A Graduate Course. 1st ed. Springer Finance. Springer-Verlag Berlin Heidelberg.
Musiela, Marek, and Marek Rutkowski. 2010. Martingale Methods in Financial Modelling. 2nd ed. 2005. Corr. 3rd printing. Stochastic Modelling and Applied Probability. Springer.